Code for: Propulsion in hexapod locomotion: How do desert ants traverse slopes?

Contents

Bibliographic Information

% Manuscript Decision - Accepted on 7 Feb 2017
% MS ID#: JEXBIO/2016/137505
% MS TITLE: Propulsion in hexapod locomotion: How do desert ants traverse slopes?
% AUTHORS: Toni Woehrl, Lars Reinhardt, and Reinhard Blickhan
% ARTICLE TYPE: Research Article
% Journal: Journal of Experimental Biology 2017 220: 1618-1625
% DOI (Data): 10.5061/dryad.j4594, published online February 22, 2017
% DOI (Article): 10.1242/jeb.137505, published online May 3, 2017

Example Video

Please click on the image below to download the video.

Prerequisites

The following two additional Matlab scripts were required to plot the figures.

Matlab version

version

ans =

8.6.0.267246 (R2015b)

Load data

Download: data.mat (5.48 MB)

close all; clear all; clc
load('data.mat')
whos

  Name         Size              Bytes  Class      Attributes

  F            6-D             2160000  double               
  d3          75x4                4594  dataset              
  data1      225x19             138924  dataset              
  data2        1x1             5138670  struct               
  p5l          1x1              120352  struct

Fig. 1A-C: Weight-specific leg impulses at different slopes

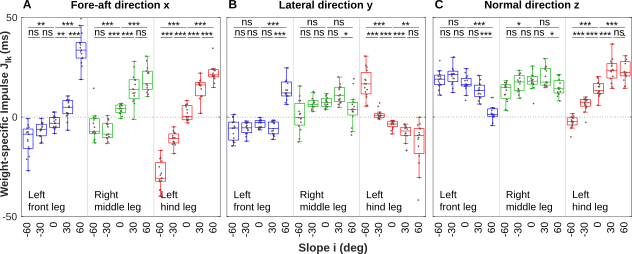
plot_data1.title     = {'Fore-aft Impulse J_x', 'Lateral Impulse J_y', 'Normal Impulse J_z'};
plot_data1.color     = [1 0 0                 ; 0 0 1                ; 0 0.7 0];
plot_data1.direction = 'xyz';

leg   = unique(data1.legnr);
slope = unique(data1.deg);

% location of horizontal lines below siginificance stars for
% pairwise comparisons
y1 = [45 45];
y2 = [40 40];  % neighbours
xd = 0.05;     % gap

% Plot
for l = 1:length(plot_data1.direction) % Direction

    % Impulse data
    clear I_l
    I_l   = eval(['data1.Impulse',plot_data1.direction(l),'BW']);

    figure(l);
    plot([0 16],[0 0],':k','LineWidth',0.5); hold on % Zero

    % Plot data points (grey) below boxplots
    for ll = 1:length(leg) % leg number

        for lll = 1:length(slope) % slope

            % subset impulse data
            clear filter_lll I
            filter_lll = logical(cell2mat(data1.legnr) == cell2mat(leg(ll)) & data1.deg == slope(lll));
            % Impulse
            I = I_l(filter_lll);

            % scatter points horizontally
            clear x lx x2
            x = (ll-1)*length(slope) + lll;
            lx = length(I);
            x2 = linspace(-.1,.1,lx);
            plot(x2+x,I,'.','Color',[1 1 1]*.7); hold all

            % horizontal lines for significance stars
            if lll==1 || lll==3
                plot([x+xd x+2-xd],y1,'k')
            end
            if lll<5
                plot([x+xd x+1-xd],y2,'k');
            end
        end
    end

    % plot boxplot
    clear bh
    bh = boxplot(I_l,{str2num(cell2mat(data1.legnr)),data1.deg},...
        'factorseparator',[1 1],...
        'labelverbosity','majorminor',...
        'medianstyle','line',...
        'notch','off',...
        'colorgroup',data1.legnr,...
        'color',plot_data1.color,...
        'factordirection','list',...
        'boxstyle','outline',...
        'outliersize',0.1,...
        'widths',.75);

    set(bh, 'markeredgecolor', [1 1 1]*.5,'Linewidth',.5, 'linestyle','-');

    axis([0.5 15.5 -50 50]);
    axis square

    title(plot_data1.title{l});
    xlabel('Slope i (deg)');
    ylabel('Weight-specific Impulse J_{lk} (ms)');

    text(1,-42, {'Left';'front leg'} ,'color','k','horizontalalignment','left');
    text(6,-42,{'Right';'middle leg'},'color','k','horizontalalignment','left');
    text(11,-42,{'Left';'hind leg'}  ,'color','k','horizontalalignment','left');

end

Fig. 2A-E: Mean GRF vectors with mean stepping patterns at different slopes

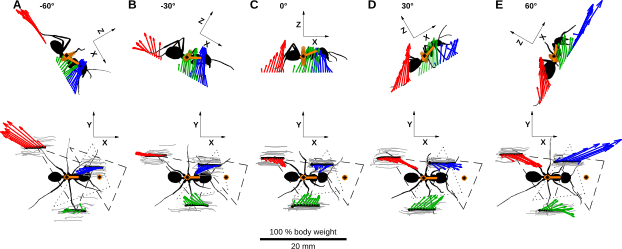
close all;

% select and order slopes
slopes = {'m60','m30','n00','p30','p60'};

% color coding of legs
cl_kk = [0 0 1; 0 .7 0; 1 0 0];

% color and linestyle supporting tripd
cl_sm = [1 1 1].*0;
ls_sm = '--';

for k = 1:length(slopes)

    % Suporting tripod: tarsus midstance positions, suporting tripod (mean)
    clear msx1 msy1 msx2 msy2 msx3 msy3
    msx1 = mean(data2.C.(slopes{k}).l1.MidStance2X,2);
    msy1 = mean(data2.C.(slopes{k}).l1.MidStance2Y,2);
    msx2 = mean(data2.C.(slopes{k}).l2.MidStance2X,2);
    msy2 = - mean(data2.C.(slopes{k}).l2.MidStance2Y,2); % middle leg lateral direction
    msx3 = mean(data2.C.(slopes{k}).l3.MidStance2X,2);
    msy3 = mean(data2.C.(slopes{k}).l3.MidStance2Y,2);

    % Displacement of petiolus (mean)
    clear dp
    dp   = mean([data2.C.(slopes{k}).l1.Displacement,...
        data2.C.(slopes{k}).l2.Displacement,...
        data2.C.(slopes{k}).l3.Displacement],2);


    % Petiolus b3
    clear b3px b3py b3pz
    b3px = [data2.C.(slopes{k}).l1.b3x,data2.C.(slopes{k}).l2.b3x,data2.C.(slopes{k}).l3.b3x];
    b3py = [data2.C.(slopes{k}).l1.b3y,data2.C.(slopes{k}).l2.b3y,data2.C.(slopes{k}).l3.b3y];
    b3pz = [data2.C.(slopes{k}).l1.b3z,data2.C.(slopes{k}).l2.b3z,data2.C.(slopes{k}).l3.b3z];

    % Head-Thorax joint b2
    clear b2px b2py b2pz
    b2px = [data2.C.(slopes{k}).l1.b2x,data2.C.(slopes{k}).l2.b2x,data2.C.(slopes{k}).l3.b2x];
    b2py = [data2.C.(slopes{k}).l1.b2y,data2.C.(slopes{k}).l2.b2y,data2.C.(slopes{k}).l3.b2y];
    b2pz = [data2.C.(slopes{k}).l1.b2z,data2.C.(slopes{k}).l2.b2z,data2.C.(slopes{k}).l3.b2z];

    % Center of mass (mean): 20 % of the thorax length
    % McMeeking, R. M.; Arzt, E. and Wehner, R. (2012). Cataglyphis desert ants improve their mobility by raising the gaster. J. Theoret. Biol. 297, 17-25.
    clear compx compy compz
    compx = [data2.C.(slopes{k}).l1.comx,data2.C.(slopes{k}).l2.comx,data2.C.(slopes{k}).l3.comx];
    compy = [data2.C.(slopes{k}).l1.comy,data2.C.(slopes{k}).l2.comy,data2.C.(slopes{k}).l3.comy];
    compz = [data2.C.(slopes{k}).l1.comz,data2.C.(slopes{k}).l2.comz,data2.C.(slopes{k}).l3.comz];

    % Mean body posture per slope and stride cycles, relative to Center of mass (x=0,y=0)
    b2px = mean(mean(b2px - compx,2));
    b2py = mean(mean(b2py - compy,2));
    b2pz = mean(mean(b2pz,2));

    b3px = mean(mean(b3px - compx,2));
    b3py = mean(mean(b3py - compy,2));
    b3pz = mean(mean(b3pz,2));

    for kk = 1:3 % legs
        hold all
        % Ground reaction force (duration,direction)
        clear GRF
        GRF(:,1)  = mean(data2.C.(slopes{k}).(['l',num2str(kk)]).Fx,2);
        GRF(:,2)  = mean(data2.C.(slopes{k}).(['l',num2str(kk)]).Fy,2);
        GRF(:,3)  = mean(data2.C.(slopes{k}).(['l',num2str(kk)]).Fz,2);

        % Petiole (duration,direction)
        clear b3x b3y b3z
        b3x = data2.C.(slopes{k}).(['l',num2str(kk)]).b3x;
        b3y = data2.C.(slopes{k}).(['l',num2str(kk)]).b3y;
        b3z = data2.C.(slopes{k}).(['l',num2str(kk)]).b3z;

        % Head Thorax joint (duration, direction)
        clear b2x b2y b2z
        b2x = data2.C.(slopes{k}).(['l',num2str(kk)]).b2x;
        b2y = data2.C.(slopes{k}).(['l',num2str(kk)]).b2y;
        b2z = data2.C.(slopes{k}).(['l',num2str(kk)]).b2z;

        % Center of mass (duration, direction)
        clear comx comy comz
        comx = data2.C.(slopes{k}).(['l',num2str(kk)]).comx;
        comy = data2.C.(slopes{k}).(['l',num2str(kk)]).comy;
        comz = data2.C.(slopes{k}).(['l',num2str(kk)]).comz;

        % Tarsi (duration, direction)
        clear p5x p5y
        p5x = data2.C.(slopes{k}).(['l',num2str(kk)]).p5x;
        p5y = data2.C.(slopes{k}).(['l',num2str(kk)]).p5y;

        % Mean Body Height
        clear BodyHeight
        BodyHeight = data2.C.(slopes{k}).(['l',num2str(kk)]).BodyHeight;


        % mirror middle leg in lateral direction
        if kk == 2
            p5y = -p5y;
            b3y = -b3y;
            b2y = -b2y;
            comy= -comy;
            GRF(:,2)  = -GRF(:,2);
        end

        figure(k)

        %%%%%%%%%%%%%%%%%%%%%%%%%
        % Dorsal view (xy plane)%
        %%%%%%%%%%%%%%%%%%%%%%%%%

        subplot(2,1,2)

        % plot tarsus trajectories with mean
        clear px py pxm pym

        px  = p5x - comx;
        py  = p5y - comy;
        pxm = mean(p5x-comx,2);
        pym = mean(p5y-comy,2);

        plot(px,py,'color',[1 1 1].*.6); hold on
        plot(pxm,pym,'k','linewidth',2);


        % Supporting tripod (spatial stepping pattern)
        % plot layer over tarsus trajectories
        if kk == 3

            % Tripod 1
            plot([msx1 msx2],[msy1 msy2],'color',cl_sm,'linestyle',ls_sm); hold on
            plot([msx1 msx3],[msy1 msy3],'color',cl_sm,'linestyle',ls_sm)
            plot([msx2 msx3],[msy2 msy3],'color',cl_sm,'linestyle',ls_sm)

            plot(dp+[msx1 msx2],[msy1 msy2],'color',cl_sm,'linestyle',ls_sm); hold on
            plot(dp+[msx1 msx3],[msy1 msy3],'color',cl_sm,'linestyle',ls_sm)
            plot(dp+[msx2 msx3],[msy2 msy3],'color',cl_sm,'linestyle',ls_sm)

            % Tripod 2
            plot(dp/2+[msx1 msx2],-[msy1 msy2],'color',[1 1 1].*.0,'linestyle',':'); hold on
            plot(dp/2+[msx1 msx3],-[msy1 msy3],'color',[1 1 1].*.0,'linestyle',':')
            plot(dp/2+[msx2 msx3],-[msy2 msy3],'color',[1 1 1].*.0,'linestyle',':')


            % Plot Thorax (Petiole -> Head-Thorax-joint)
            plot([b3px b2px],[b3py b2py],'color',[1 .5 0]*1,'linewidth',2)

            % Plot Displacement
            plot(0,0,'o','MarkerFaceColor',[1 .5 0]*1,...
                'MarkerEdgeColor',[1 .5 0]*1,'Markersize',4);
            plot(0,0,'*k','Markersize',3);
            plot(dp,0,'o','MarkerFaceColor',[1 .5 0]*1,...
                'MarkerEdgeColor',[1 .5 0]*1,'Markersize',4)
            plot(dp,0,'*k','Markersize',3)

            % Center of triangle
            % spx = (msx1 + msx2 + msx3)/3;
            % spy = (msy1 + msy2 + msy3)/3;
            % plot(spx,spy,'dg','MarkerFaceColor','g') % center of triangle

            % Scale force-space 20x
            plot([-18 2],[18 18],'k','LineWidth',2)
            text(-9,18.5,'100 % BW','VerticalAlignment','bottom',...
                        'HorizontalAlignment','center')
            text(-9,17.5,'20 mm','VerticalAlignment','top',...
                        'HorizontalAlignment','center')
        end

        % plot ground reactio force vectors
        for kkk = 5:10:95
            quiver(pxm(kkk),pym(kkk),GRF(kkk,1)*20,GRF(kkk,2)*20,...
                'color',cl_kk(kk,:),'LineWidth',1,...
                'MaxHeadSize',.5,'AutoScaleFactor',1);
        end

        xlabel('x (mm)')
        ylabel('y (mm)')
        axis([-22 25 -22 25])
        axis square


        %%%%%%%%%%%%%%%%%%%%%%%%%%
        % Sagittal view xz-plane %
        %%%%%%%%%%%%%%%%%%%%%%%%%%

        subplot(2,1,1)

        % Body height
        clear s
        s = scatter(zeros(length(BodyHeight),1),BodyHeight,...
            'filled','SizeData',15,...
            'markerfacecolor',[1 .5 0]*.8);
        alpha(s,.5)

        % Ground reaction force vectors
        for kkk = 5:10:95
            quiver(pxm(kkk),0,GRF(kkk,1)*20,GRF(kkk,3)*20,...
                'color',cl_kk(kk,:),'LineWidth',1,...
                'MaxHeadSize',.5,'AutoScaleFactor',1);
        end

        % Thorax axis (Petiole Head-Thorax-joint)
        % plot layer as last layer
        if kk == 3
            plot([b3px b2px],[b3pz b2pz],'color',[1 .5 0]*1,'linewidth',2)

            % Scale force-space 20x
            plot([-18 2],[18 18],'k','LineWidth',2)
            text(-9,18.5,'100 % BW','VerticalAlignment','bottom',...
                        'HorizontalAlignment','center')
            text(-9,17.5,'20 mm','VerticalAlignment','top',...
                        'HorizontalAlignment','center')
        end

        xlabel('x (mm)')
        ylabel('z (mm)')
        axis([-22 25 -22 25])
        axis square

    end
end

Fig. 3A-C: GRF over time

close all
%figure(1)
figure('Name','test', 'Units', 'normalized', 'Position', [0,0,1,1])
ha = tight_subplot(9,5,[0.01 0.01]*2,[0.03 0.01]*2,[0.03 0.03]*2);

% constant of free fall
g = 9.81; % [kg*m/s^2]
clear slopes
slopes = unique(data1.deg);

% range green stripes
ay1 = [1 1 1]*-.75;
ay2 = [1 1 1]*.75;

% color double support durations
dscol = [0 .7 0];

% color leg
cl_kk = [0 0 1; 0 .7 0; 1 0 0];

for k = 1:length(slopes) % slopes

    % filter for subsets
    clear filter_k
    filter_k = data1.deg==slopes(k);

    % Gait cycle duration
    time     = data1.GaitCycleDuration(filter_k); % time in s

    % normalised stance duration per slope (middle legs, normalised)
    time_stance     = data1.TimeStance2(filter_k)./time*100; % in percent %
    time_stance_m   = mean(time_stance);

    for kk = 1:3 % legs
        filter_kk = data1.deg==slopes(k) & str2num(cell2mat(data1.legnr))==kk;

        for kkk = 1:3 % directions

            clear fq fqm fq1 fq2

            % Force
            % Tripod 1
            % F(degs,legs,tripod,direction,time,sample)
            fq   = squeeze(F(k,kk,2,kkk,:,:));
            fqm = mean(fq,2);

            % Tripod 2
            fq2   = squeeze(F(k,kk,1,kkk,:,:));
            fqm2 = mean(fq2,2);

            % plot
            ak =   k + 15*kkk - 15 + 5*kk - 5;
            axes(ha(ak));

            hold all
            box on

            fill([50 time_stance_m time_stance_m 50 50],...
                [ay1(kkk) ay1(kkk) ay2(kkk) ay2(kkk) ay1(kkk)],...
                [1 1 1]*.7,'EdgeColor',dscol,'FaceColor',dscol,...
                'FaceAlpha',.2,'EdgeAlpha',0); hold all
            fill(100+[50 time_stance_m time_stance_m 50 50],...
                [ay1(kkk) ay1(kkk) ay2(kkk) ay2(kkk) ay1(kkk)],...
                [1 1 1]*.7,'EdgeColor',dscol,'FaceColor',dscol,...
                'FaceAlpha',.2,'EdgeAlpha',0)
            fill([100 50+time_stance_m 50+time_stance_m 100 100],...
                [ay1(kkk) ay1(kkk) ay2(kkk) ay2(kkk) ay1(kkk)],...
                [1 1 1]*.7,'EdgeColor',dscol,'FaceColor',dscol,...
                'FaceAlpha',.2,'EdgeAlpha',0)
            fill(-100+[100 50+time_stance_m 50+time_stance_m 100 100],...
                [ay1(kkk) ay1(kkk) ay2(kkk) ay2(kkk) ay1(kkk)],...
                [1 1 1]*.7,'EdgeColor',dscol,'FaceColor',dscol,...
                'FaceAlpha',.2,'EdgeAlpha',0)

            % plot standard deviation
            stdshade(fq',1,'k',[1 1 1]*0.6,[1:length(fq)]); hold on



            % tripod 2
            plot([1:length(fqm)],fqm2,'LineStyle','-','LineWidth',.4,...
                'Color',[0 0 0]); hold on
            % tripod 1
            plot([1:length(fqm)],fqm,'LineStyle','-','LineWidth',1.2,...
                'Color',cl_kk(kk,:)); hold on

            % plot title only for first six subplots
            if ak < 6
                title([num2str(slopes(k)),'°'],'FontWeight','normal', ...
                    'FontSize',10)
            end
            axis square
        end

    end
end

set(ha([1:5:45]),'YTickLabel',{'-0.5','0','0.5'},'YTick',[-0.5,0,0.5],'TickLength',[0.05,0.05])
set(ha(40:45),'XTickLabel',{'0','','100'},'XTick',[50,50 + time_stance_m,150],...
                         'XTickLabel',{'0','','100'},'XTick',[50,50 + time_stance_m,150],...
                     'TickLength',[0.05,0.05])
set(ha,'TickDir','in');
set(ha,'Xlim',[0 170],'Ylim',[-.75 .75])

xlabel(ha(43),'Stride cycle right middle leg (%)')

ylabel(ha(6),'Fore-aft GRF (BW)','FontWeight','normal', 'FontSize',10,'linewidth',.5)
ylabel(ha(21),'Lateral GRF (BW)','FontWeight','normal', 'FontSize',10,'linewidth',.5)
ylabel(ha(36),'Normal GRF (BW)','FontWeight','normal', 'FontSize',10,'linewidth',.5)


% label leg right axis
set(ha([5:5:45]),'yaxislocation','right')
yl = {'{\color{blue}L1} + R1', '{\color[rgb]{0,0.7,0}R2} + L2', '{\color[rgb]{1,0,0}L3} + R3',...
      '{\color{blue}L1} + R1', '{\color[rgb]{0,0.7,0}R2} + L2', '{\color[rgb]{1,0,0}L3} + R3',...
      '{\color{blue}L1} + R1', '{\color[rgb]{0,0.7,0}R2} + L2', '{\color[rgb]{1,0,0}L3} + R3',...
     };

ik = 0;
for k = 5:5:45
    ik = ik + 1;
    set(get(ha(k),'YLabel'),'String',cell2mat(yl(ik)),'FontSize',10,'FontWeight','normal','linewidth',.5);
end

Fig. 4A-D: Comparison of the mean GRF vectors on upslopes and downslopes

close all

% color leg pair
cl_kk = [1 .7 0;0 0 1;0 .7 0];
% compare slopes
deg_pair = [-60,60;-30,30];
% force-space ratio
fscale = 20;
% axis
axis_vec=[-19 19 -19 19];
% midstance (mean of range between 49 to 51, [1:100])
meanwindow = 49:51;
% scale settings
force_scale_text = '50 % body weight';
space_scale_text = '10 mm';
scale = [-9,-9 + fscale*.5];
% changing linewidth for vectors
lw = linspace(1,.1,105);

for m = 1:2 % plot layers
    %(individual measurements below mean and below force)

    for l = 1:2 % slope pair

        clear degs
        degs = deg_pair(l,:);

        for k = 1:length(degs); % selected slope

            for kk = 1:3 % legs

                clear filter_kk

                filter_kk = data2.deg==degs(k) & data2.leg == num2str(kk);

                % 1 Tarsi
                % Anterior extreme positions aep
                % static supporting triangle
                clear aepx aepy aepz pet50x pet50y pet50z
                aepx = mean(data2.p5x(1:2,filter_kk))-mean(data2.b3x(1:2,filter_kk));
                aepy = mean(data2.p5y(1:2,filter_kk))-mean(data2.b3y(1:2,filter_kk));
                aepz = -mean(data2.b3z(1:2,filter_kk));

                % 2 Location of Petiole during midstance
                % (relative to petiole location during touchdowns)
                pet50x = mean(data2.b3x(meanwindow,filter_kk))-mean(data2.b3x(1:2,filter_kk));
                pet50y = mean(data2.b3y(meanwindow,filter_kk))-mean(data2.b3y(1:2,filter_kk));
                pet50z = mean(data2.b3z(meanwindow,filter_kk))-mean(data2.b3z(1:2,filter_kk));


                % ground reaction force
                clear fx fy fz
                fx  = mean(data2.Cx(:,filter_kk),2)*fscale;
                fy  = mean(data2.Cy(:,filter_kk),2)*fscale;
                fz  = mean(data2.Cz(:,filter_kk),2)*fscale;

                % mirror lateral direction if leg == middle leg
                if kk == 2
                    pet50y=-pet50y;
                    aepy = -aepy;
                    fy = -fy;
                end

                % one figure per slope pair
                figure(l);

                % one subplot for each plane (xy versus xz)
                subplot(2,1,1)


                % Colors
                clear colo
                if (degs(k) < 0 && kk == 1)
                    colo = [0 0 1];
                elseif (degs(k)  > 0 && kk == 1)
                    colo = [0 0 0.3];
                elseif (degs(k)  < 0 && kk == 3)
                    colo = [1 0 0];
                elseif (degs(k)  > 0 && kk == 3)
                    colo = [0.3 0 0];
                elseif (degs(k)  < 0 && kk == 2)
                    colo = [0 .7 0];
                else
                    colo = [0 .7 0]*.3;
                end
                % plot annotations and individual measurements
                % below mean and force
                if m == 1

                    % plot origin of coordiante system
                    plot(0,0,'ok')

                    % plot petiole mean+-std (crosses)
                    plot(pet50x,pet50y,'.','color',[1 1 1].*0)

                    % plot anterior extreme position
                    plot(aepx,aepy,'+','color',[1 1 1]*.5)
                else

                    plot(mean(aepx)+std(aepx)*[1 -1],mean(aepy).*[1 1],'k','Linewidth',1.5)
                    plot(mean(aepx)*[1 1]           ,mean(aepy)+std(aepy)*[1 -1],'k','Linewidth',1.5)

                    % plot force
                    for kkk = 1:5:length(fx)
                        quiver(mean(aepx),mean(aepy),fx(kkk),fy(kkk),'Color',colo,'MaxHeadSize',.8,'AutoScaleFactor',1,...
                            'Linewidth',lw(kkk)); hold on
                    end

                    xlabel('x (mm)')
                    ylabel('y (mm)')
                    axis(axis_vec)
                    axis square
                end

                % xz-plane
                subplot(2,1,2)

                % plot annotations and individual measurements
                % below mean and force
                if m == 1

                    % plot origin of coordinate system
                    plot(0,0,'ok')

                    % plot scale
                    text(-9+(scale(2)-scale(1))/2,-9,force_scale_text,...
                        'FontSize',10,'VerticalAlignment','top',...
                        'HorizontalAlignment','center'); hold on
                    text(-9+(scale(2)-scale(1))/2,-9,space_scale_text,...
                        'FontSize',10,'VerticalAlignment','bottom',...
                        'HorizontalAlignment','center'); hold on
                    plot(scale,[-9, -9],'k','LineWidth',0.5)


                    % plot petiole mean+-std (crosses)
                    plot(pet50x,pet50z,'.','color',[1 1 1]*0)

                    % plot anterior extreme position
                    plot(aepx,aepz,'+','color',[1 1 1].*.5)


                else

                    % plot mean anterior extreme position
                    plot(mean(aepx)+std(aepx)*[1 -1],mean(aepz)*[1 1],'k','Linewidth',1.5)
                    plot(mean(aepx)*[1 1]          ,mean(aepz)+std(aepz)*[1 -1],'k','Linewidth',1.5)

                    % plot force
                    for kkk = 1:5:length(fx)
                        clear ah
                        quiver(mean(aepx),mean(aepz),fx(kkk),fz(kkk),'Color',colo,'MaxHeadSize',.8,...
                            'AutoScaleFactor',1,'Linewidth',lw(kkk)); hold on
                    end

                    xlabel('x (mm)')
                    ylabel('z (mm)')
                    axis(axis_vec)
                    axis square
                end
            end
        end
    end
end

Fig. 5A-B: Hind leg dragging and change of body height

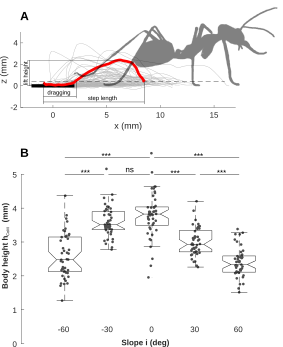
Fig. 5A: Hind leg dragging

close all

% sample trajectory in red
sam = 36;

% Uncertainty
xmin = 0.4; % [mm]

% Hind leg Tarsus trajectories
x = p5l.x;
% zero vertical component
z = p5l.z - repmat(mean(p5l.z(1:2,:)),100,1);

% Plot
% trajectories
plot(x,z,'color',[1 1 1]*.7,'LineWidth',.5); hold on
% uncertainty line
plot([-2 16], [xmin xmin],'--k')
% force plate
plot([-2 2], [0 0],'k','Linewidth',5)
% sample trajectory in red
plot(x(:,sam),z(:,sam),'r','Linewidth',4); hold all
axis equal
axis([-3 17 -2 5 ])
xlabel('x (mm)')
ylabel('z (mm)')
shg

Fig. 5B: Change of body height

close all; clear bh
% create dataframe for bodyheight
bh.BodyHeight = data2.BodyHeight';
bh.leg        = num2str(data2.leg);
bh.deg        = data2.deg;

clear slopes
slopes = unique(bh.deg);
figure(1)
for k = 1:5 % plane
    % subset data
    clear filter_k dat_k lx x2
    filter_k = logical(bh.deg == slopes(k));
    dat_k = bh.BodyHeight(filter_k);
    % scatter and plot data
    lx = length(dat_k);
    x2 = linspace(-.1,.1,lx);
    plot(x2+k,dat_k,'.','Color',[1 1 1]*.3,'Markersize',10); hold on
end

boxplot(bh.BodyHeight,bh.deg,...
    'labelverbosity','majorminor',...
    'medianstyle','line','notch','on',...
    'boxstyle','outline','factordirection','list',...
    'symbol','+k','outliersize',0.1,'widths',.75);

xlabel('Slope i (deg)')
ylabel('Body height (mm)')

Fig. 6A-C: Normalised double support durations for each leg pair at different slopes

close all

% stride duration middle leg per definition gait cycle duration
clear sd slopes
sd = data1.td22 - data1.td12;
slopes = unique(data1.deg);

for k = 1:3 % legs
    clear dat
    % normalise double support durations
    % by stride duration of the middle legs
    dat   = eval(['data1.ds',num2str(k)])./sd*100;
    figure(k)

    for kk = 1:length(slopes) % slopes

        % subset data
        filter_kk = data1.deg == slopes(kk);
        dat_kk = dat(filter_kk);

        % scatter and plot data
        lx = length(dat_kk);
        x2 = linspace(-.1,.1,lx);
        plot(x2+kk,dat_kk,'.','Color',[1 1 1]*.3,'Markersize',10); hold on

    end

    % plot boxplot over scatterd data
    bh = boxplot(data1.(['ds',num2str(k)])./sd*100,data1.deg,...
        'labelverbosity','majorminor',...
        'medianstyle','line','notch','on',...
        'boxstyle','outline','factordirection','list',...
        'symbol','.','outliersize',0.1,'widths',.75,'color',[0 0 0]);

    xlabel('Slope i (deg)')
    ylabel('Duration (%)')

end

stepx: stepping length in mm dx: dragging length in mm dz: tarsus lift heights in mm

grpstats(d3,'deg','median','DataVars',{'stepx','dx','dz'})

ans = 

           deg    GroupCount    median_stepx    median_dx    median_dz
    -60    -60    15            6.8024          6.8264       0.42321  
    -30    -30    15            7.7551           7.767         0.774  
    0        0    15            9.1626          9.1626         0.996  
    30      30    15             8.574           8.574        1.0428  
    60      60    15            8.4687          8.4687         1.443

Table 4: Kinematic parameter

data1.Duty2       = data1.TimeStance2./data1.TimeStep2*100; % Duty factor
data1.TimeStep2   = data1.TimeStep2.*1000;   % Stride duration of the middle legs in ms
data1.TimeStance2 = data1.TimeStance2.*1000; % Contact duration of the middle legs in ms
data1.GaitCycleVelocity2 = data1.GaitCycleVelocity2.*1000; % Running speed in mm/s
% Displacement of the CoM per stride of the middle legs in mm/Stride
data1.GaitCycleDisplacementS2 = data1.GaitCycleDisplacementS2.*1000;
grpstats(data1,'deg',{'mean','std'},'DataVars',...
    {'TimeStep2','TimeStance2','Duty2','GaitCycleVelocity2','GaitCycleDisplacementS2'})

ans = 

           deg    GroupCount    mean_TimeStep2    std_TimeStep2
    -60    -60    45            127.87            29.746       
    -30    -30    45            108.98            14.082       
    0        0    45            109.91            12.634       
    30      30    45            135.87            22.504       
    60      60    45            168.98            19.751       


           mean_TimeStance2    std_TimeStance2    mean_Duty2    std_Duty2
    -60    93.067              29.362              71.69        7.2404   
    -30    68.622              15.391             62.429        7.8164   
    0      68.933               10.75             62.681        6.1896   
    30     89.778              19.974             65.672        5.6179   
    60     114.44               20.23             67.483        6.8958   


           mean_GaitCycleVelocity2    std_GaitCycleVelocity2
    -60    63.777                     25.275                
    -30    83.723                     26.113                
    0      87.362                     17.402                
    30     70.642                     14.593                
    60     53.673                     9.6925                


           mean_GaitCycleDisplacementS2    std_GaitCycleDisplacementS2
    -60    7.7211                          1.9294                     
    -30    9.0467                          2.0994                     
    0      9.6601                          1.5619                     
    30     9.4821                          1.1748                     
    60     9.0547                          1.2206

Table 4: Body Height (Center of mass - substrate distance in mm)

data3.deg        = data2.deg;
data3.BodyHeight = data2.BodyHeight';
grpstats(dataset(data3),'deg',{'mean','std'},'DataVars','BodyHeight')

ans = 

           deg    GroupCount    mean_BodyHeight    std_BodyHeight
    -60    -60    45             2.582              0.6612       
    -30    -30    45             3.596             0.45271       
    0        0    45            3.7922             0.67355       
    30      30    45            3.0065             0.41909       
    60      60    45             2.399             0.43189

Body Height (Petiole - substrate distance in mm)

grpstats(data1,'deg',{'mean','std'},'DataVars','BodyHeightMean')

ans = 

           deg    GroupCount    mean_BodyHeightMean    std_BodyHeightMean
    -60    -60    45            2.1749                 0.61942           
    -30    -30    45            3.2094                 0.45431           
    0        0    45            3.4913                 0.65939           
    30      30    45            2.7155                 0.40139           
    60      60    45             2.116                 0.41245


Published with MATLAB® R2015b

This item was created on 2018-07-23 and last modified on 2019-09-20.